今回は、ラマンスペクトルを定量的に評価するために欠かせないピークフィットについて解説します。 まずどのようにピーク形状関数を選ぶのかについて説明した後、ピーク強度、ピーク位置、半値幅の定量的な解析方法について説明します。

ピーク形状関数の選び方

ピークフィッティング処理とは、測定したピークに対して、誤差が最も小さくなるようにピーク形状を求めることです。 そのためには、まず元になるピーク形状関数を選ぶ必要があります。 代表的なピーク形状関数には、ローレンツ関数とガウス関数があります。 それぞれの式を以下に示します。 これらの式の中で、強度（A）、位置（x0）および幅（w）の3つのパラメータを決めることでピーク形状が決まることが分かると思います。 同じ条件でピーク形状を比較すると、以下のようなピーク形状の違いがあることが確認できます。

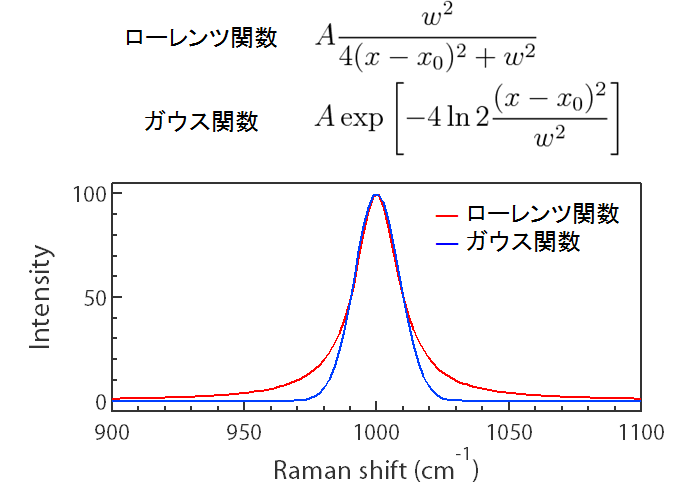
ラマンスペクトルの形状は理想的にはローレンツ関数となりますが、測定試料が非晶質な場合には振動モードがガウス関数的に広がっていくことが多くなります。 そのため、材料やその状態に合わせて適切なピーク形状を選ぶことになります。 また、ローレンツ関数とガウス関数の畳み込みによって得られるフォークト関数もピークフィットに用いられます。 フォークト関数は、ピーク形状がローレンツ関数とガウス関数のどちらにもならずその中間にある場合に用いられます。

ピーク強度の定量評価

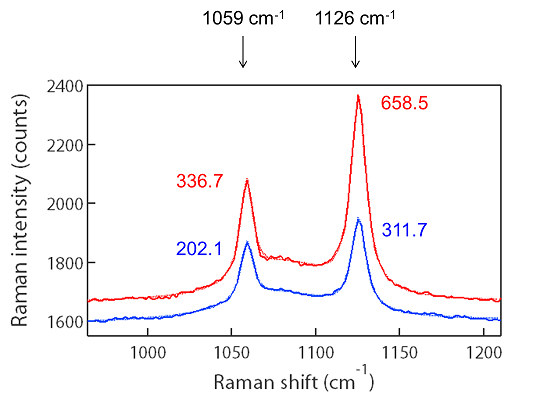
単独ピークで重なりがない場合にはピーク強度はスペクトルから簡単に読み取れますが、ピークが重なっている場合にはピークフィット解析をする必要があります。 以下に、延伸したエージーピールフィルムの配向を評価するために、ピーク強度比を評価した例をご紹介します。

評価したいピークは以下のスペクトルの1059cm^-1と1126cm^-1のピークですが、その間にブロードが小さいピークが乗っています。 そのため3つのピークの重ね合わせとしてそれぞれのピーク強度を求めるのが確実な評価方法になります。 下図では、実線が生データ、点線がフィッティング結果になっており、3つのピーク（ローレンツ関数）によって良い一致が得られています。 それぞのピーク強度は図中に示してある通りの値となり、その結果、ピーク強度比I₍₁₁₂₆₎/I₍₁₀₅₉₎はそれぞれ1.96と1.54であることが求められました。

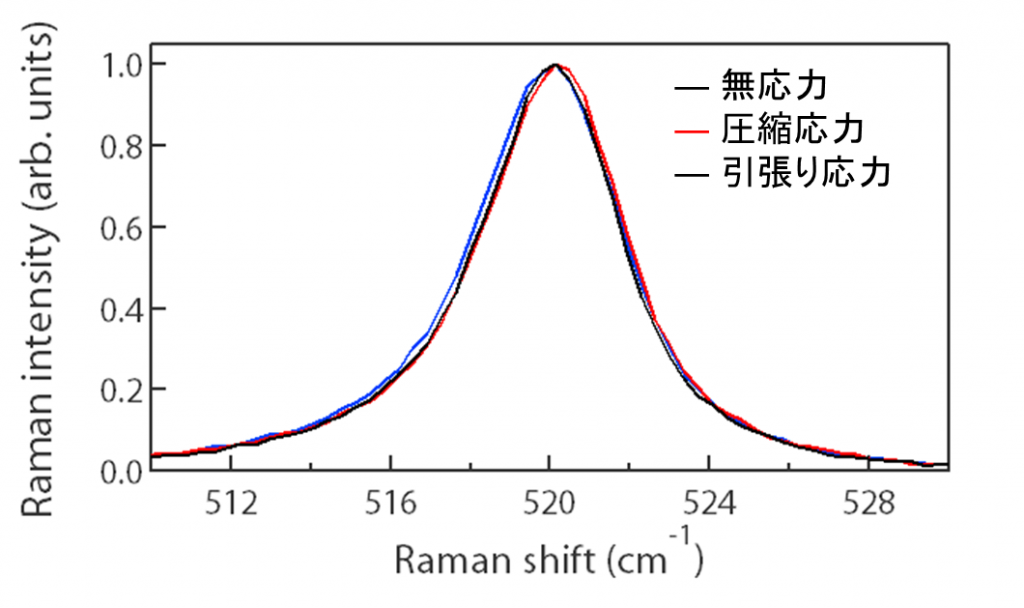
ピーク位置の定量評価

材料に生じている応力を評価する場合には、応力が無い状態でのピーク位置とのピークシフト量を評価します。 半導体や高分子などの材料によらず、ピークシフト量は応力と線形な関係があるので、ピークシフト量を正確に求めるためにピークフィットを用います。 以下にシリコン基板の応力を評価した例をご紹介します。 グラフは無応力の箇所と引張り、圧縮の応力が生じている箇所でのラマンスペクトルです。 ピークトップの位置だけ見るとピーク位置の変化はないように見えますが、ピーク位置が若干異なっています。 これを、ピークフィッティングにより計算すると、それぞれのピーク位置は、519.94cm^-1, 520.00cm^-1, 520.09cm^-1であることが求められました。

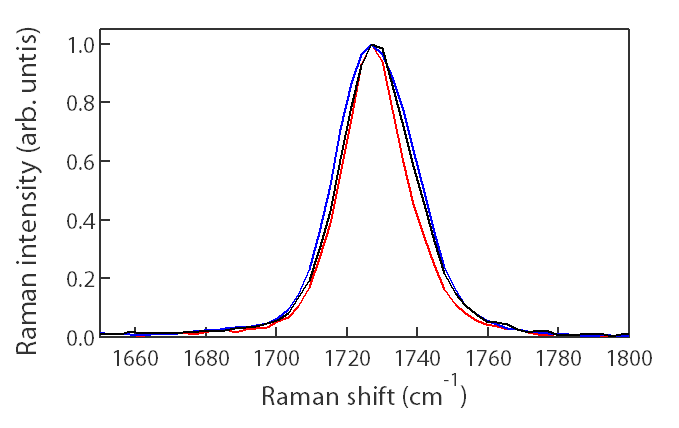
半値幅の定量評価

半値幅は、高分子や半導体の結晶性評価を評価する際に用いられる指標です。 例えば高分子であれば、半値幅は密度と相関があることが知られています。 以下にPETの結晶性を評価した例をご紹介します。 ペットボトルの位置によってPETの結晶性は異なっており、それらの変化はC=Oの結合に帰属される1730cm^-1のピークによって評価できることが知られています。 下図のピークでは、半値全幅（FWHM）はそれぞれ22.4cm^-1, 24.9 cm^-1, 26.6cm^-1と求められました。 また、ピークフィットの際には、材料が非晶質であるためガウス関数によってフィッティングを行いました。